Welcome to the Circle of Fifths Lesson!
Use the previous and next buttons to traverse through the lesson.
Click the interactive buttons in the lesson text to enhance your learning.

× Home Lesson: Notes Quiz: Notes Quiz: Steps Lesson: Scales Quiz: Scale Identification Quiz: Scale Construction Quiz: Interval Lesson: Staff Lesson: Circle Quiz: Key Signature Reference Guide
☰ Menu
z
C
s
C# Db
x
D
d
D# Eb
c
E
v
F
g
F# Gb
b
G
h
G# Ab
n
A
j
A# Bb
m
B
q
C
2
C# Db
w
D
3
D# Eb
e
E
r
F
5
F# Gb
t
G
6
G# Ab
y
A
7
A# Bb
u
B
i
C
9
C# Db
o
D
0
D# Eb
p
E

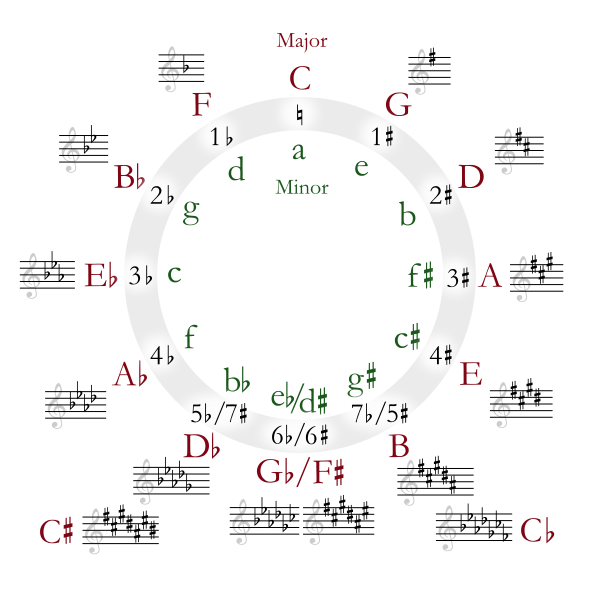
For this lesson, we will begin by displaying a chart.
This is known as the Circle of Fifths, a chart displaying the relationships between all 12 possible notes.
Let’s focus on the outer layer of the circle first.
Starting with C at the top of the chart, each adjacent note is located a perfect fifth interval away as you travel around the circle clockwise.
G is a perfect fifth away from C. D is, in turn, a fifth away from G. This process repeats until we return to C.

The key signatures beside their respective notes represent the major key built off the note. For instance, the key of C has no sharps or flats, as denoted by the key signature.
The next note, the G, has one sharp in its key signature, which is notably a difference of one accidental from the key of C.
So it makes sense that the key of D major (two fifths away from C) has two sharps, which is a two-accidental difference from C major.

The same principle applies in a counterclockwise direction, but with flats instead of sharps, and fourths instead of fifths.
F is one fourth away from C, and therefore the key of F major has one flat-- a one accidental difference from C major.
The key of Bb has two flats, the key of Eb has three, etc
The bottom of the circle is the note Gb (or its enharmonic equivalent F#) which has either 6 flats or 6 sharps in its major key depending on which enharmonic equivalency is defined.

Now, the interior circle.
The inner circle works just like the outer one, but with minor keys.
The relative minor key of C major is A minor, as denoted on the circle.
As E is a perfect fifth away from A, the key of E minor has one sharp, just as G major.
A simple way to find the relative minor key of a major key is to simply go three semitones down from the tonic note. C->B->Bb->A (illuminate keys)

The circle of fifths has applications beyond memorizing key signatures.
In popular music, chord progressions generally travel in very small steps around the circle.
For instance, the most natural resolutions of a chord progressions travel in fifths. One of the most ubiquitous progressions in music, the ii V I, is powerful due to the very natural resolution of the V -> I, a perfect counterclockwise fifth on the circle.
Putting chord progressions in the context of the circle of fifths offers a very visual and geometric perception of how chords interact with each other in proximity to the tonic note of the key.
Now, let’s go to the quiz.